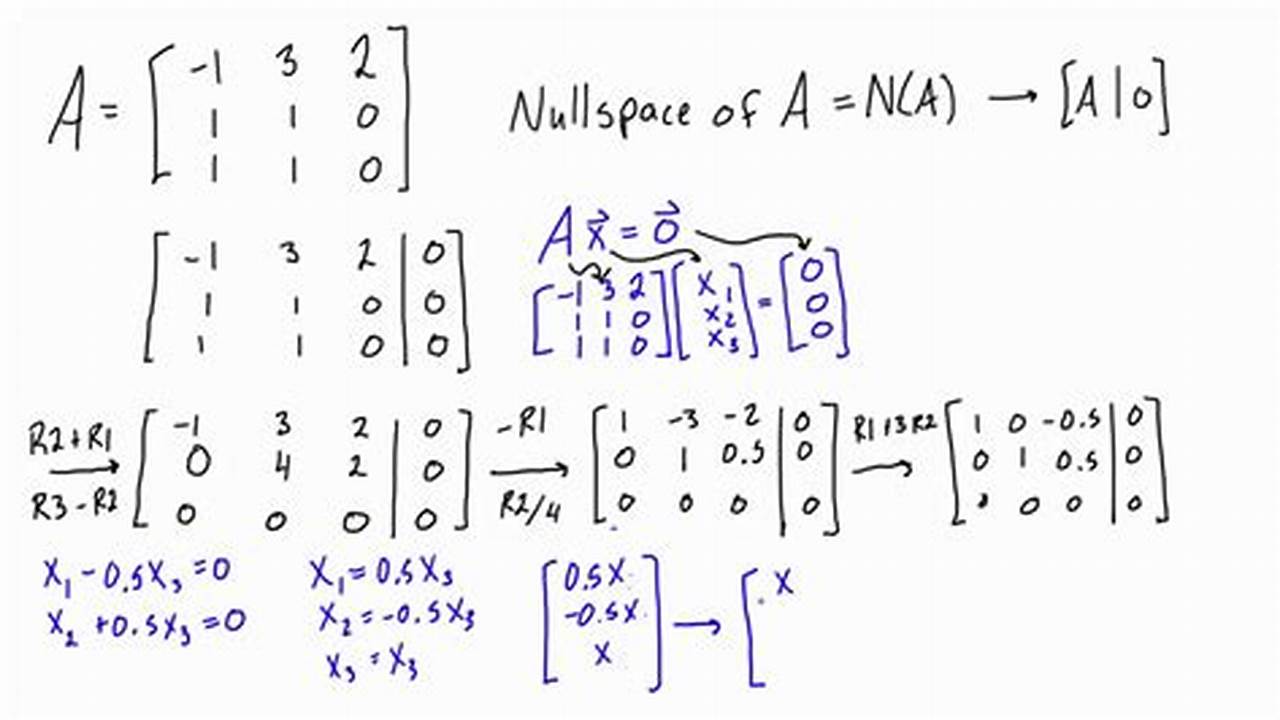
In linear algebra, the null space or kernel of a matrix is the set of all vectors that are mapped to the zero vector by the matrix. It is a subspace of the vector space of all possible input vectors. The null space of a matrix is important because it can be used to find the solutions to a system of linear equations. If the null space of a matrix is non-zero, then the system of equations has infinitely many solutions.
To find the null space of a matrix, we can use the following steps:
